入試問題

息子と一緒に風邪をひいてしまい、
貴重な休日を１日寝て過ごしてしまった澤井秀太郎です。
2人して、1日で回復したのでめでたしめでたしです。

さて、前回までかけ算・わり算についてと、さらにものごとの意味を考えることの大切さを述べてまいりましたが、
今回は入試問題についてです。

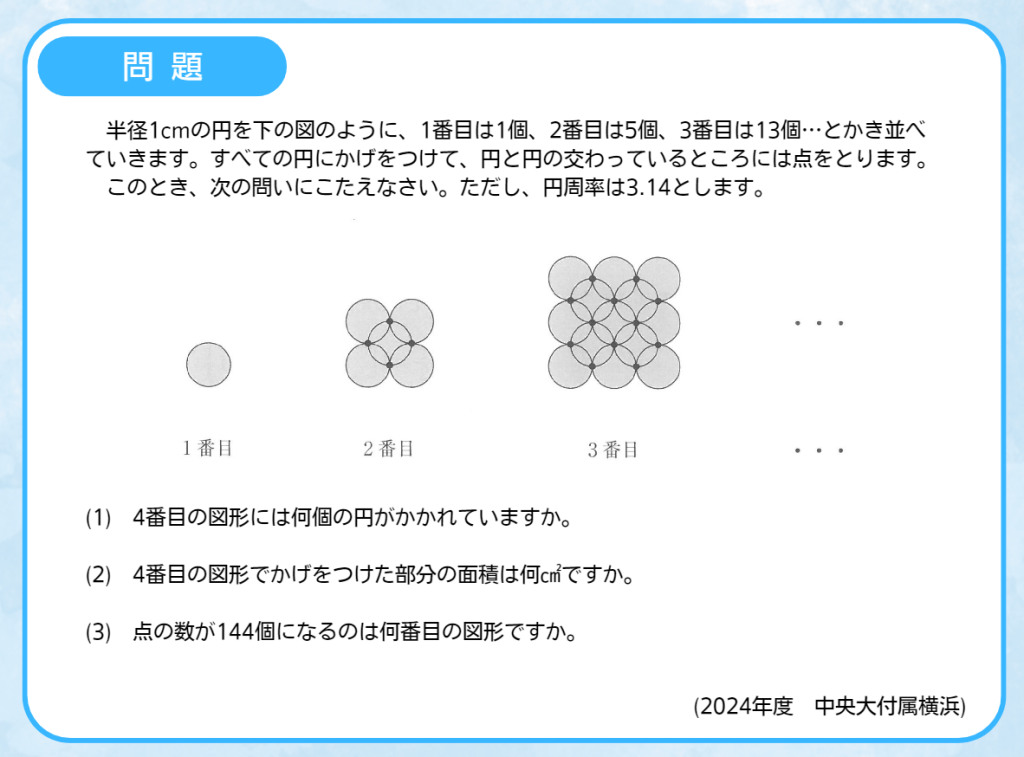
さっそく、問題です。

いかがでしょうか。

ぱっと見、どう考えるべきか、わかりにくくなっています。
でも、丁寧に作業を進めていくことで、(3)まで小学5年生の夏までに学習する内容で解ききることができるんです。

解答・解説はあえてここには書きませんが、考えるヒントを出しておきます。

(1)は、方陣算の考え方を使います。
方陣算とは、ご石を正方形や長方形・三角形の形になるように置いたときのご石の数を考える問題です。
ここではご石を正方形の形に置いたときの１番外側のご石の数を考えていくことで、正解にたどりつけます。
もちろん、自分で3番目の図に円を書き足していって、全部で円が何個になるか数えても構いません。

(2)は、円やおうぎ形を含む面積を求める問題です。
いくつかの図形が合わさってできた複合図形を切り分けるなどして、自分の知っている（面積を求められる）形にしていくことがポイントです。
この問題では、正方形をひとつと、いくつかのおうぎ形に分けます。
おうぎ形も、この問題ではほとんどが半円になります。
複数の半径が等しいおうぎ形の面積は、中心角を合計すると計算しやすくなります。
また、3.14をかける計算は、分配法則を使って3.14を最後にかけるようにすると、計算ミスが少なくなり、スピードも上がります。

(3)は、これも方陣算の考え方を使います。
交点をご石にみたてて、さらに分割すると、同じ三角形の形に並べるものがいくつかできます。
これを何番目まで並べれば全部で144個になるのかを考えます。
最後に落とし穴もあるので、気を付けて取り組んでください。

こういう問題がすらすらとではなくとも解けるのであれば、素晴らしいです。
特に5年生で解けるのであればなおさらです。

こういう応用問題も実は基本の積み重ねで解けるようになります。
基本の考え方を、その意味や理屈から理解できていると、どうしてその考え方を使うのかということもわかりやすくなり、
似たような問題を解く際の力になります。

解答・解説はこちらのリンクからご確認ください。

　解答・解説