問題にチャレンジしてくれてありがとうございます。

では、さっそく解答から。

(1)　25個
(2)　47.98㎠
(3)　9番目

いかがでしたか？

5年生でこれができていたら、本当にすごい！　自信をもって夏期講習で、さらに力を伸ばしてください。
できなかったからダメということもありません。
どう考えればよかったのか、そこのところを確認して、解き方のキモを増やしていきましょう。

 

では、次に解説です。

(1)は方陣算です。

方陣算は「予習シリーズ」では、4年生の夏期講習で学習しました。
ご石を四角形や三角形の形に並べて、全体の数やいちばん外側の数を求める問題です。

この問題は円を重ねているので、ご石に見えないのですが、ご石を並べる問題の考え方を利用します。

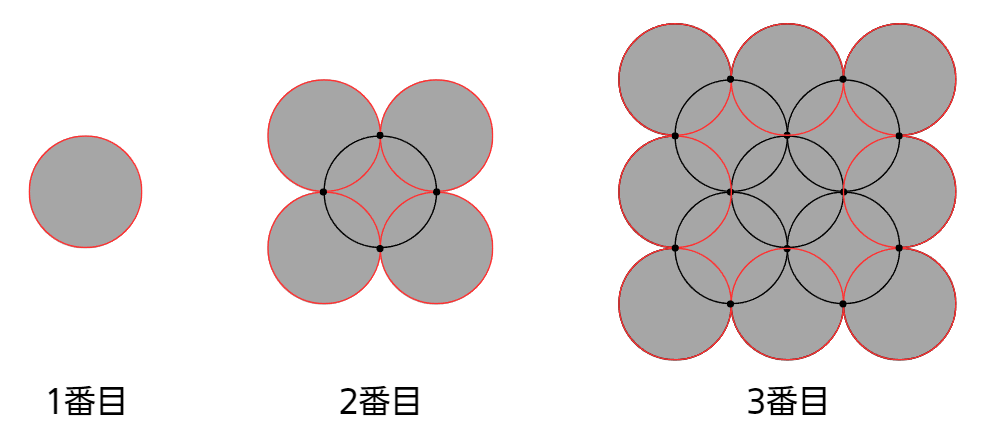
下の図1を見てみましょう。

＜図1＞

ご石を正方形の形に並べたときの、いちばん外側の数を考えてみます。
図1の一番外側の円（赤い円）は正方形の形に並んでいます。1辺の円の数はN番目と同じです。
1番目は1個、2番目は4個、3番目は8個です。
ここでうっかり平方数なのかな？　と勘違いしないように気をつけましょう。

4番目のいちばん外側の1辺の円の個数は4個です。
ですので、方陣算の考え方を使うと

（4ー1）×4＝12

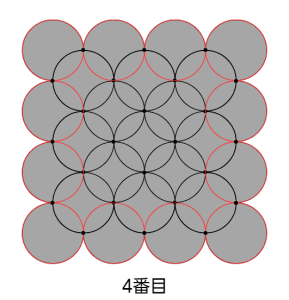
となるので、いちばん外側の円の個数は12個です。（図2）

ですので、3番目までの1＋4＋8＝13に4番目の12個をたして、25個になります。

＜図2＞

 

続いて、(2)です。

これは平面図形の面積を求める問題ですね。
複数の図形が組み合わさった図形を複合図形といいます。
複合図形の面積は、どのように切り分けて自分の知っている形を作るかがポイントです。

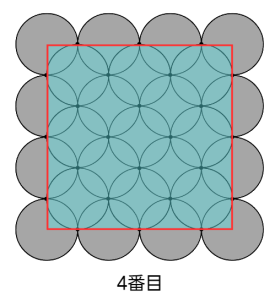
この問題では（図３）のようにするとわかりやすいでしょう。

＜図3＞

いちばん外側の円の中心をとおるように、正方形を書きます。

すると、正方形の外側におうぎ形がいくつかできますね。
この正方形とおうぎ形全部の面積の和が答えになります。

正方形の1辺の長さは円3個分の直径と同じですから、6㎝です。
ですので、正方形の面積は

6×6＝36㎠

おうぎ形は半円が8個と中心角270度のおうぎ形が4つで、合計の中心角は

180×8＋270×4＝2520度

です。

これ、もう少し簡単にすると、半円が8個で円が4個分
円の3/4（4分の3）が4つで　3/4×4＝3　なので、円3個分
あわせて円7つ分となります。

2520/360　とするより簡単ですね。

半径1㎝の円が7個の面積なので、

1×1×3.14×7＝21.98㎠

となります。
で、うっかりやりやすいのがこれを答えにしてしまうこと。
（ぼくもうっかりやってしまうことがあります。みなさん気を付けましょう）
はじめに切り取った正方形の面積を足さないとですね。

36＋21.98＝47.98㎠

これが正解です。

ちょっと脱線しますが、3.14×1から3.14×9までは九九のように暗記してしまうと計算が楽になります。
また、平方数（同じ整数をかけた数）も11×11から19×19までは覚えておくと役立ちます。

 

さあ、最後の(3)です。

じつはこれも方陣算の考え方を使います。
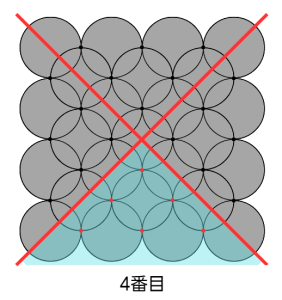
まずは（図４）を見てみましょう。

＜図４＞

4番目の図形で考えるとわかりやすいので、この図になっています。

図形を（図４）のように4等分します。
すると、円と円の交わっているところの点も4等分されます。

そのうちの1つを見ると、ご石を三角形の形に並べているのと同じですね。
1段増えるごとにご石が1個ずつ増えています。
これ、等差数列の考え方とも同じですね。

点の数が全部で144個になるとき、4等分したひとつの三角形の点の数は

144÷4＝36個

です。
1段増えるごとにご石が1個ずつ増えていって36個になるのは何段目かを考えます。
方陣算でも等差数列でも同じ式になります。

（1＋□）×□÷2＝36

ですね。
ここで、　（1＋□）×□　が　36×2　で72になることがわかります。

この後はどうしますか？
72を素因数分解してください。

72＝2×2×2×3×3

ですね。この素因数の積の組み合わせで差が1になるようにします。
すると、　9×8　がでてきます。

9×8＝（1＋8）×8

なので、8段目まで並べたときが、点の数が144個になるときです。

ここでも注意点があります。

円と円の交わる点が初めて出てくるのは２番目の図形です。

1番目の図形は点が0個、2番目は4個、3番目は12個・・・

となります。
2番目の図形から8番目なので、

1番目をたして、

8+1＝9番目

となるのです。

どうでしょう。

今までに学んできたことで解くことができないことはないという問題でしたね。
しかも、使っている公式なども基本どおりです。

いかに基本が大切か。そして、その基本のうち、何を使ったら問題が解けるのかという
解き方のパターンを知ることも大事です。

解き方のパターンは基本がしっかり身についていれば6年生の秋からで十分間に合います。

5年生はとにかく基本の反復、6年生も基本がまだあやしければこの２学期しっかりと基本を使えるレベルまで磨き上げましょう。