円周率が3.14なのはなぜ？

こんにちは！

3月20日。今日は春分の日です。

立春からおよそ1月半というのに、昨日は吹雪のような雪降り。

まだまだ寒い日が続きますね。

息子はというと、大好きな「おしりたんてい」の映画を観に行ったようで、

にっこにこの写真がLINEで送られてきて、僕までうれしくなりました。

観に行けてよかったね。

さて、今回は算数の話題です。

円周率として、小学生は3.14を使います。

でも、なんで3.14なの？　と疑問はありませんでしたか？

今ではコンピューターを使って100兆けたまで求められているようですが、

算数でそれを使うわけにはいきませんから、近似値をとって3.14としています。

では、そもそも円周率が3.14であることはいつ頃求められたのでしょう。

それは古代ギリシャの数学者アルキメデス（紀元前287年ごろ～紀元前212年ごろ）だといわれています。

アルキメデスは円の内側と外側に接する正多角形をかき、

辺の長さの和と円周の長さをくらべました。

円周の長さは内側の多角形の辺の和より長く、

外側の多角形の辺の和より短いことを利用して、おおよその値を計算しました。

より正確な値までしぼりこむためには円に近い正多角形で調べる必要があるため、

正96角形を使ったそうです。

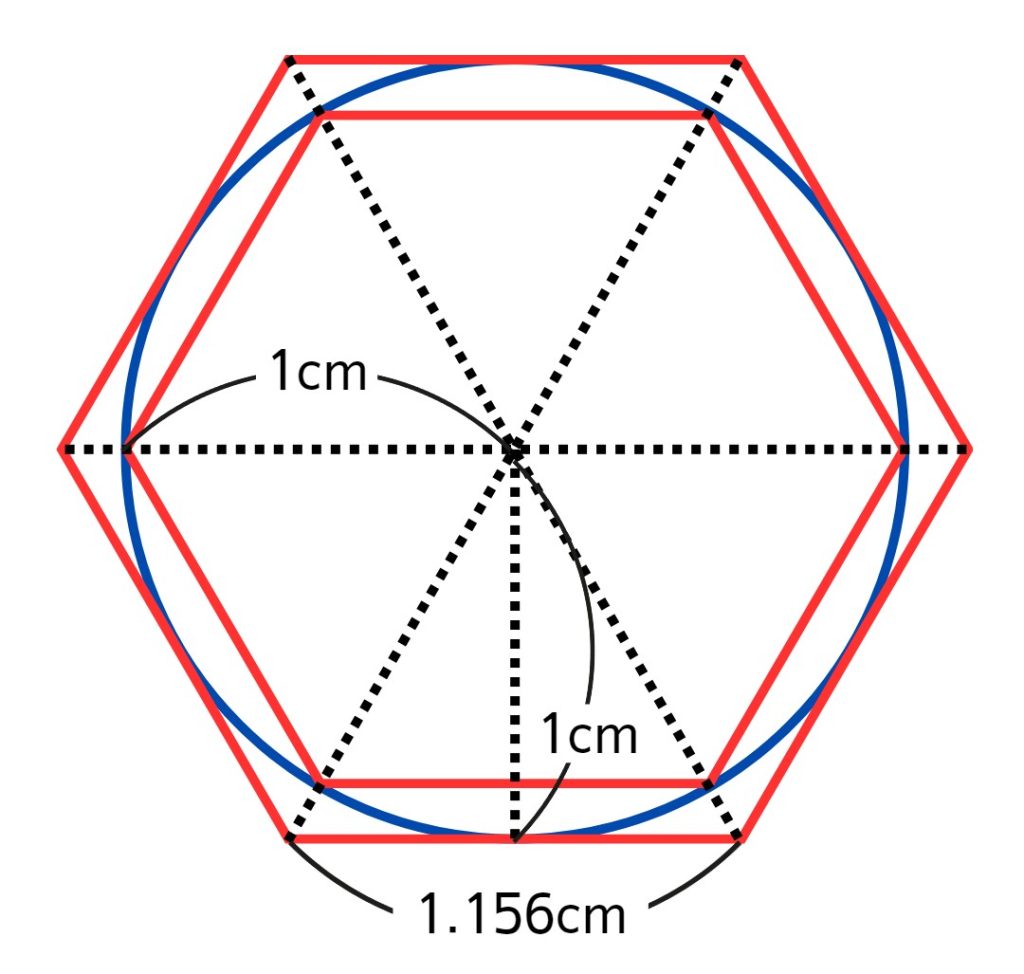
この考え方を正六角形を使って考えるとしたの図のようになります。

半径1cmの円の内側と外側に接する正六角形を書きました。

内側の六角形の1辺の長さは1cmになるので、まわりの長さは6cm。

外側の六角形の1辺の長さが（これは中学生で学ぶ知識を使うのですが、）

約1.15cmで、まわりの長さは6.9cm。

円の直径は2cmなので、それぞれ2でわると

内側が3、外側が3.45となり、

円周率は3から3.45の間となります。

これをアルキメデスさんは正96角形まで計算して、3.14を求めたということです。

小学生でも円周率が3より大きいことは理解できるはずです。

ちなみに円周率は、たとえば、陸上競技で使われる走路トラックで、

選手のスタート位置を決めるのに使われます。

陸上競技場ではトラックの曲線の部分は半円になっていますが、

レーンが外側に向かうにつれて半径が大きくなり、

同じ位置からスタートすると、走る距離がのびてしまいます。

そこで円周率を使ってレーンごとに半円の長さを求め、

その差の分だけスタート位置をずらすことで、

どのレーンを走っても距離が同じになります。

公式を覚えてさえいれば計算はできますが、

公式がどのようにして作られたのか、その意味を考えながら使ってみると

楽しくなりますね。

他のいろいろな公式も意味を考えながら使うことで、

色々な問題についてより深く理解できるようになります。